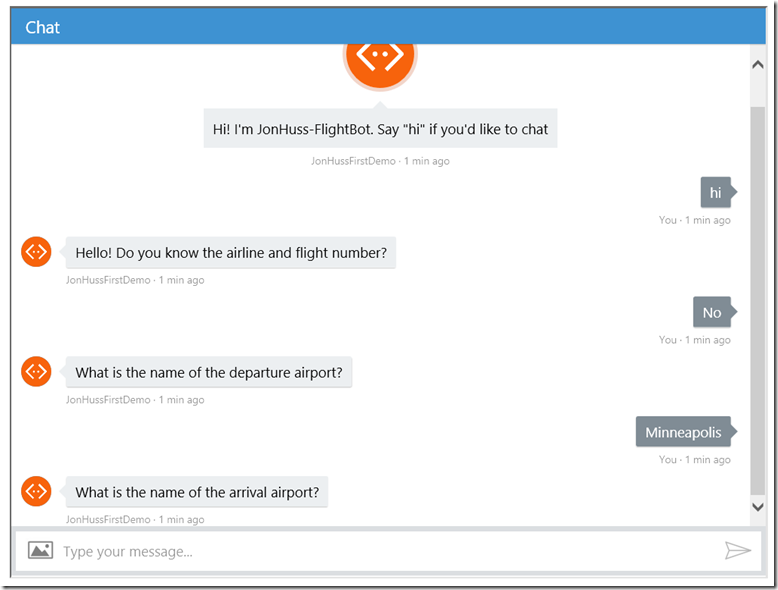
Recently I spent some time out in Redmond with some folks and we discussed Microsoft’s new Bot Framework quite a bit.  At the time, I had already started to explore the framework, but certainly didn’t (and still don’t) know enough.  I’ve been exploring it further every day since.  To that end, I’ve been working on a demo bot (to be shared in the near future) that looks up airline flight data.  One of the steps asks the user to choose from a list of international airports – some 8,000 of them.  It’s routed to the user via the PromptDialog.Choice(…) dialog.  The airports are simply passed as a list to the options parameter of the function.  This works great in Visual Studio.  However, once I deployed it out to Azure for actual testing, the process fell over (which is exactly why demo’ing all the way is important!).  When the bot asked for the departure airport via the PromptDialog.Choice(…) dialog and the user responded, the bot simply reverted back to the original, introductory “Hello!  Welcome to the flight bot!” question in the process.  What?!  What in the world?

Troubleshooting

Knowing that there are a ton of airports in the list, I first wondered if it was somehow related to that list – specifically the count.  That didn’t really make a ton of sense, because it’s not like we were bumping up against an Integer limit or something. I really thought it was more likely an issue with the size of the message.  However, I tried reducing the number of items to 50 anyway just to see what would happen.  Plus, if it was an issue with the size of the message, changing the count would have an impact.  Sure enough, it worked fine.  I played around with it some more and discovered an upper limit of about 650 airports before things stopped working.

Now that I knew that the problem was somehow directly related to the airport list, and it didn’t really make sense for it to be related to the count, I focused on the message size.  After all, the Bot Framework just runs on top of a Web API service (at least in the C# version), which would be subject to the various request message size limits.  I tried reducing the amount of data that was attached to each airport record.  That also had an impact – I could now send 1500 or so airports back and forth without issue.  At this point, I was confident that the problem was related to the size of the messages.

My understanding of the Bot Framework is that the bot itself runs inside of Microsoft’s Bot engine, which is ultimately rendered in a website (assuming the bot is running in a web page).  The Bot engine makes calls out to our Web API service for the various interactions.  As such, there are two web sites that could potentially be running into size restrictions.  I only have access to my service, so I tried updating the system.web/httpRuntime/maxRequestLength of my web service to it’s maximum value.  No dice.  At this point, my assumption is that the message/state is being serialized back to the client, but that not all of the data is available (either because an exception was thrown or because it was cut off), and so the response just results in the dialog starting over.

Since the limit is apparently inside of the Bot engine (maybe just via IIS config or something simple), and I don’t have access to that, the next step is to try and implement an alternative.

The alternative

As far as I can tell, the real benefit to sending a list of options is that the Bot Framework will automatically attempt to match the user’s response to the list of options and return that matching object.  Luckily for us, the nice folks that are part of the Bot Framework team provided the source code for the Bot Builder classes, including the PromptDialog class, so that we can go investigate how it works.  That particular class is here: https://github.com/Microsoft/BotBuilder/blob/master/CSharp/Library/Dialogs/PromptDialog.cs.

If we make our way to the PromptChoice<T> class within that file, we can see that all that’s really happening is that the TryParse function scores the response against each of the potential options and then selects the option with the highest score.  Looks simple enough to reproduce.

I ended up just creating a MatchHelper class that totally borrows the TryParse and ScoreMatch functions from the PromptChoice<T> class.  I modified the functions slightly so that they would accept a Func that allows them to search against particular properties on the option, rather than just using the .ToString() results to match.  The resulting helper looks like this:

using System;
using System.Collections.Generic;
using System.Linq;
 
namespace FlightBot.Helpers
{
    public class MatchHelper
    {
        public virtual Tuple<bool, int> ScoreMatch(string option, string input)
        {
            var trimmed = input.Trim();
            var text = option.ToString();
            bool occurs = text.IndexOf(trimmed, StringComparison.CurrentCultureIgnoreCase) >= 0;
            bool equals = text == trimmed;
            return occurs
                ? Tuple.Create(equals, trimmed.Length)
                : null;
        }
 
        public bool TryParse<T>(IEnumerable<T> options, Func<T, string> propertyFunc, string text, out T result)
        {
            if (!string.IsNullOrWhiteSpace(text))
            {
                var scores = from option in options
                             let score = ScoreMatch(propertyFunc(option), text)
                             select new { score, option };
 
                var winner = scores.Where(s => s.score != null).OrderBy(s => s.score).First();
                if (winner.score != null)
                {
                    result = winner.option;
                    return true;
                }
            }
 
            result = default(T);
            return false;
        }
    }
}

Now that this utility is available, I can switch my code from calling Prompt.Choice to calling Prompt.Text and then sending the text based results into the utility.  The resulting set of calls looks like this:

public async Task GetDepartureAirport(IDialogContext context, IAwaitable<Airport> argument)
{
    PromptDialog.Text(context,
                        GetArrivalAirport,
                        "What is the name of the departure airport?",
                        "I don't understand.  What is the name of the departure airport?");
}
 
 
 
public async Task GetArrivalAirport(IDialogContext context, IAwaitable<string> argument)
{
    string providedAirport = await argument;
 
    _departureAirport = MatchAirport(providedAirport);
 
    PromptDialog.Text(context,
                        GetFlightDate,
                        "What is the name of the arrival airport?",
                        "I don't understand.  What is the name of the arrival airport?");
}
 
private Airport MatchAirport(string airportName)
{
    List<Airport> airports = GetAirports();
 
    MatchHelper matchHelper = new MatchHelper();
    Airport matchedAirport = null;
    if (matchHelper.TryParse(airports, a => a.Name, airportName, out matchedAirport))
        return matchedAirport;
    else
        return null;
}

Working through this code, GetDepartureAirport asks the user for the name of the departure airport, the results from the user are returned to the GetArrivalAirport function and are then passed into the MatchAirport function which uses our utility to parse the results.  By using this alternative method, we completely bypass having to send the full list of airports to the user and things are back to working as expected.  Sweet!

Thoughts?

This was my way of solving my problem.  How would you have solved it?  Is there a better way that I just don’t understand yet?  Is there some kind of configuration setting that I didn’t find?  I’d love to hear your feedback telling me that I’m way out in left field and there’s a simpler solution.